
データサイエンス超入門、Excelで求める相関係数。
卒論のために、本を読みまくっていてブログを放置してしまいました。書きたいことは山ほどあるのだけど。
さて、データサイエンティストなどデータの専門家、統計学の知識を持つ人たちに注目が集まっている昨今、ものごとの関係性を根拠を持って言いたいときに役立つのが相関係数!です。
それでは、相関係数を分析するための方法を解説します。
*ちなみに相関係数は、0が相関なし。1に近づくほど、相関が強い。つまり、Aという事象とBという事象は一緒に起こりやすい。(Aが高いときは、Bも高い。)、逆に-1に近づくほど、負の相関が強い。つまり、Aという事象と、Bという事象は一緒に起こりにくい。(Aが高いときは、Bは低い。)という、-1〜1の間で示される値です。
目次
1、データの準備
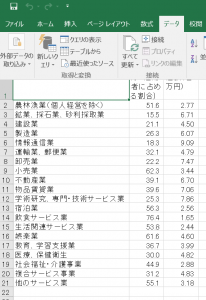
今回のデータは、A列が「各業種」、B列が「非正規職員比率(役員を除く雇用者に占める割合)」、C列が「一人当たり付加価値額(百万円)」を示しています。
Excelファイルは、総務省統計局の「社会人のためのデータサイエンス入門」のダウンロードファイルより。
https://lms.gacco.org/asset-v1:gacco+ga031+2016_03+type@asset+block/week1-6.xlsx
2、データ分析のアドインを準備する
相関を分析するためには、この矢印の先に「分析ツール」を表示させる必要があります。この準備のために、まず「分析ツール」のアドインを入れる必要があります。
*Macは、Excel2016から分析ツールのアドインが用意されています。それ以前のExcelでは、StatPlus:mac LEというツールで対応できるようです。
「ファイル」をクリック。

「オプション」をクリックして、Excelオプション画面へ。
「アドイン」をクリックして、「設定(G)…」をクリックし、アドイン画面へ。
「分析ツール」にチェックを入れて、「OK」をクリック。
![]()
これで、「データ」タブに「データ分析」が出現する。
3、データの相関係数を求める
![]()
「データ分析」をクリックしデータ分析画面へ。
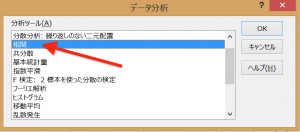
「相関」をクリックして、「OK」をクリックし相関画面へ。
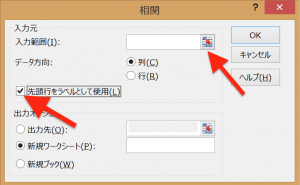
「先頭行をラベルとして使用」にチェックを入れて、「入力範囲(I):」のボタンをクリックして範囲設定へ。
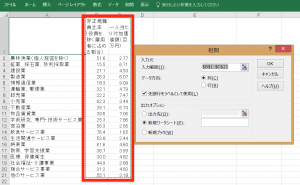
列の先頭を含めて範囲を選択する。選択後、相関画面の「OK」をクリックすると、シートが生成され相関係数が求められる。
![]()
この場合は、-0.7でした。
結果は、
B列「非正規職員比率(役員を除く雇用者に占める割合)」と、C列「一人当たり付加価値額(百万円)」には、負の相関がある。
です。
言い換えれば、
B列「非正規職員比率(役員を除く雇用者に占める割合)」高いとき、C列「一人当たり付加価値額(百万円)」は低い。
と言えます。
取り扱いの注意としては、相関関係は、因果関係ではないので、事象の時間的な順序は特定できません。因果関係を示すには、実験による観察が必要です。
先ほどの、非正規職員比率と一人当たり付加価値額で言えば、「非正規職員比率を高めると、一人当たり付加価値額が下がってしまう。」とは、言えないということです。
逆の「一人当たり付加価値額が低いから、非正規職員比率が高い。」可能性もその他の可能性もあるので、どっちが先なのかは、この相関係数だけでは特定できません。
このように、ある事象の関係性を示す相関関係は、データ分析で使用できるととってもかっこいいですが、因果関係との区別をしっかりして使うといいと思います。
相関関係と因果関係について簡単に説明すると、
例、5000人の集団の中に、コーヒーを飲む人が2500人いました。コーヒーを飲まない2500人とコーヒーを飲む2500人の寿命を比べると、コーヒーを飲む人の方が、平均5年長生きでした。
この、コーヒーを飲む人の集団と、その寿命の長さは相関関係があると言えます。
一見、「コーヒーを飲めば、寿命が長くなる」ような因果関係があるのではないかという気がしてきますが、他の要因で長生きな母集団の食生活や文化に、たまたまコーヒーを飲む習慣があるだけという可能性を否定できません。
つまり、コーヒーの成分や飲むこと自体に、寿命を長くする効果があるかどうか不明です。
因果関係を調べるには、コーヒーを飲んでいない集団から、無作為にコーヒーを飲む集団をつくり、無作為に選ばれたコーヒーを飲まない集団との比較から、寿命を記録していくような実験をしなければなりません。
これから、IoTが発展や他のテクノロジーの開発が進み、データにアクセスするコストが下がれば、「データを得られないから分析できない」という言い訳ができなくなります。
個人レベルでも、データの取り扱い技術を身につけないと!と、最近かなり焦りはじめました。。
スギヤマです。
主にガジェットいじりに関わる記事を投稿します。






この記事へのコメントはありません。